MICRO MURDER: But It’s Robots So It’s OK has a deformable map (that is, you can dig holes in it) that spans multiple screens and all the collisions seem to be per pixel – the holes on the map are not limited to tile boundaries and can be of any radius (and theoretically any shape). On a modern platform (or, even a platfrom from past, as in the original Worms was an Amiga game) it would be a very simple task: store the whole map in memory as a huge bitmap and read and write from it as you please.

On a PICO-8 this is a bit more complicated task: the machine doesn’t have enough memory for having much more than a single screen’s (128×128) worth of pixels in an array and even if it did, it would be very slow to draw pixel by pixel from the array to the screen memory.

Instead, we need to combine a few things, old and new, and apply a liberal amount of smoke and mirrors.

Checking for pixels

We start the collision checking by simply using the map. Using mget() to check for tiles is of course pretty much PICO-8 101 stuff and we can add a single step to also check pixel inside the tile:

function checkpixel(x, y)
 -- transform screen coordinates to tile
 -- coordinates (8x8 tiles)
 x = x / 8
 y = y / 8

 local tile = mget(x, y)

 if tile == 0 then
  -- the tile is not set so we know
  -- there will be no pixels
  return false
 end

 -- manually check if the pixel
 -- inside the map tile is non-zero

 -- 1. find out the pixel coordinate inside 
 -- the tile. it's what's after the decimal dot
 -- scaled to tile size (8x8 pixels)

 local sx = (x - flr(x)) * 8
 local sy = (y - flr(y)) * 8

 -- 2. find out the top-left corner of the tile
 -- inside sprite memory

 local tx = tile % 16 * 8
 local ty = flr(tile / 16) * 8

 if sget(sx + tx, sy + ty) == 0 then
   -- the pixel was zero
   return false
 end

 -- there were no empty pixels
 -- so it was a hit!

 return true
end

We can now easily check every pixel inside the map. But, how do we edit the map pixel per pixel? It’s quite simple:
we just store all the holes (circles) made by projectiles and separately check if the coordinate is inside the hole.

function checkhole(x, y)
 for hole in all(holes) do
  local dx = x - hole.x
  local dy = y - hole.y
  if dx * dx + dy * dy <= hole.r * hole.r then
   return true
  end
 end
 return false
end

If we found a pixel that isn’t inside a hole, the projectile explodes and we simply add a new hole at the coordinates (with a variable radius).

So, here’s the whole thing in short:

1. Check for if there’s a tile at the coordinate
2. Check if the coordinate is inside a hole
3. Check if the tile has a pixel at the “sub-tile coordinate”

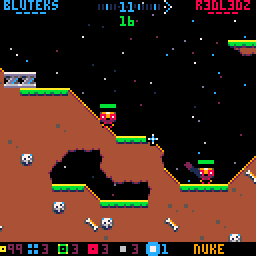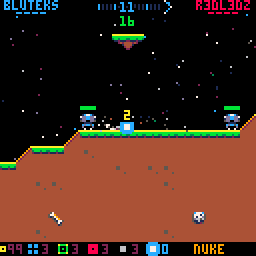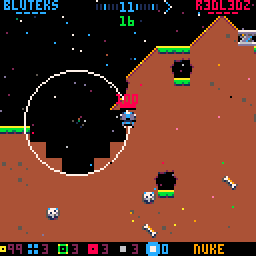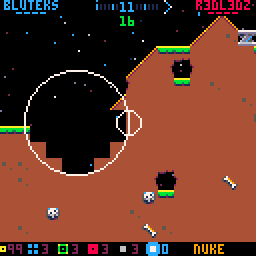
Holes are drawn as white circle outlines instead of filled black circles

Note that in the above screenshot also tiles that are fully inside holes are set to empty for speed (we don’t need to check for the individual pixels because we know the whole tile is destroyed).

if checkpixel(projectile.x, projectile.y) and 
 not checkhole(projectile.x, projectile.y) then
 -- BOOM!
 add(holes, {x=projectile.x, y=projectile.y, radius=10})
end

For speed, you might want to experiment by changing the order of the checks, depending on exact circumstances. Also, you will want to use a more efficient way to store the holes if you have thousands of them.

Bouncy bombs

In MM:BIRSIO, there are projectiles that collide with the map and seem to bounce quite accurately according to the slope at the collision point. How to find out the angle from the map pixels?

This is easy: you can get a normal vector by scanning the pixels surrounding the collision point and building a vector that is the sum of the vector pointing from the collision point to the scanned pixel:

-- dx,dy = normal vector at collision point
local dy=0
local dx=0

-- scan the surrounding area, 2 pixels to any direction
for sy=-2,2 do
 for sx=-2,2 do
  if not checkpixel(collision_point.x + sx,collision_point.y + sy) then
   -- found an empty pixel, add vector sx,sy to dx,dy
   dx += sx
   dy += sy
  end
 end
end

-- normalize dx,dy
local d = sqrt(dx * dx + dy * dy)
dx /= d
dy /= d

-- proceed with the usual reflection vector 
-- calculations etc.
-- ...

This is of course just an approximation but it works perfectly fine for our purposes. And, in case of collisions, the ground probably is uneven and has tiny rocks and so on so the bounce would not be mathematically perfect.

Drawing the map

You have probably realized that we have a tiny problem if we draw the map on screen like this (assuming a black background):

cls()

-- draw the untouched, original tiles
map()

-- draw the holes over the tiles
for hole in all(holes) do
 circfill(hole.x, hole.y, hole.radius, 0)
end

The above code will draw the map and holes correctly but you are now limited to a plain black background. If you draw a background before drawing the map over it, as you usually would, the holes would clearly be just black circles stamped against the background. This would ruin the illusion of having a huge, per pixel map.

In MM:BIRSIO, we simply add more smoke: instead of having some magic to make the holes somehow invisible, the starfield is drawn after the map – we manually check the pixel color and decide if the star would be behind the map or visible. This trick would probably be too slow for a full background (drawn pixel by pixel) but for a handful of pixels it’s perfectly fine.